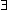 ), meaning that there exists some value for which
the predication is true.
), meaning that there exists some value for which
the predication is true.
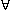 ), meaning the predication is true for all values
the variable may assume.
), meaning the predication is true for all values
the variable may assume.
Prolog is an acronym for "PROgramming in LOGic" - so named because the language is based on the predicate calculus, and was originally developed in conjunction with work on automated theorem proof, though it is now used for a broad variety of purposes.
Prolog was developed in 1972 by Alain Colmeraur and Philippe Roussel of the AI Group (Groupe d'Intelligence Artificielle) of the University of Marseille, with the collaboration of Robert Kowalski of the University of Edinburgh. It was developed in conjunction with research on automatic proving of theorems.
As various implementations of Prolog were produced, a variety of dialects emerged.
Prolog is the principal representative of the declarative programming language paradigm. Whereas imperative and functional languages are based on theoretical models of computation (the Turing machine and the Lambda Calculus, respectively), in declarative programming, one states what is to be accomplished, and lets the system figure out how it is to be accomplished. The underlying theoretical model is the predicate calculus, and computation is accomplished by means of a proof procedure that finds a way to satisfy a goal by, in effect, proving a theorem!
For example, if one desired to sort a list into ascending order (using some transitive ordering relationship such as <), one might proceed along the following lines:
One can now sort the list by, in effect, proving the theorem "there exists a sorted list that is a sorting of my given original list" - the proof procedure not only shows that this is true, but also discovers what that list is.
This reasoning yields the following Prolog program, which can successfully sort a list:
sort(List, SortedList) :- permutation(List, SortedList), isSorted(SortedList). isSorted(List) :- List = [ _ ]. % List has exactly one element - always sorted isSorted(List) :- List = [ First, Second | Rest ], First @=< Second, isSorted([ Second | Rest ]). permutation([], []). permutation(OriginalList, PermutedList) :- member(First, OriginalList, Remainder), permutation(Remainder, PermutedRemainder), PermutedList = [ First | PermutedRemainder ]. member(Element, [ Element | ListMinusElement ], ListMinusElement). member(Element, [ First | Rest ], [ First | RestMinusElement ]) :- member(Element, Rest, RestMinusElement).(There is one fly in the ointment here, however. This program is based on a strategy called generate and test - generate all possible solutions, and test each in turn until one is found that solves the original problem. Alas, in the case of sorting a list of N items, there are N! permutations. Since N! is O(2N), this algorithm has exponential complexity, and is impractical for any list of more than 10 or so items!) (It is, however, possible to write more efficient sorting algorithms in Prolog, at the expense of losing some of the elegance of a purely declarative approach.)
A key distinction between declarative languages and imperative languages lies
in the notion of a variable. An imperative language variable is vary-able - at
different points in the computation it typically takes on different values, and
its value can be changed at any point by assignment. A declarative language
variable is actually a mathematical variable - it either stands for some
as yet unknown value which is to be discovered, or for all possible values.
This distinction can be seen by noting that the statement x = x + 1,
while perfectly meaningful in a language like C or Java, is a mathematical
absurdity - there is no x for which this is true! (This is why some imperative
languages use a distinctive symbol for assignment - e.g. := as
used in Pascal or Ada.)
Prolog programs are constructed from objects called terms, which are of three basic types: atomic terms (constants), structures, and variables.
Most Prolog implementations provide three types of atomic term.
athis_Is_A_2nd_Atom
A - begins with an uppercase lettera+ - includes a non-alphanumeric character
+ - * / ~ < > = \ ` ^ : . ? @ # $ & % - e.g.
+=..
$a - includes both types of character
! ; [] {} and, in some contexts, , .
').
(A single quote may be included in the list by doubling it) - e.g.
'This book is john''s'
1-123
3.06.02e23-1.5
A Prolog structure consists of an atom followed immediately by a left
parenthesis (with no intervening space), a list of arguments separated by
commas, and a right parenthesis. The atom is called the functor
of the structure, and the number of arguments is called its arity.
For example, the following is a Prolog structure with functor
dog and arity 3: dog(snoopy, beagle, owner(brown)).
Note that an argument of a structure may itself be a structure.
In Prolog documentation, one often finds structures referred to by functor
and arity - e.g. the above example could be denoted as being of the type
dog/3. Sometimes, the documentation will refer to an atom as if
it were a structure of arity 0 - e.g. the atom dog may be
referred to as dog/0.
Though the structure is the only structured type in Prolog, the IO facility supports three different representations for structures. The latter two are simply a syntactic convenience - the internal representation for a structure is always the same.
-a is equivalent to the structure -(a)2+2 is equivalent to the structure +(2, 2)
(2+2)*(1+4) is equivalent to the structure
*(+(2,2), +(1,4)) - parentheses are used to override the
default priorities which would make 2+2*1+4 (without using
parentheses) equivalent to +(+(2, *(2, 1)), 4).
++ as in C-family languages, one
could use the builtin predicate op as follows:
op(100, yf, ++), after which x++ would be
recognized as equivalent to ++(x). (Note: though the IO
system provides for postfix operators, there are no builtin postfix
operators in most implementations.) [,
]) are used instead of parentheses, a vertical bar
(|) is used instead of a dot, and the empty list is denoted
by the atom [] instead of nil. A list is
equivalent to a sequence of structures of type ./2 - e.g.
the following are equivalent: [ this, is, a, list ] and
.(this, .(is, .(a, .(list, [])))), and the following are
equivalent [ improper | list ] and .(improper,
list).
|) is often used
to separate the first part of the list from the rest of the list, which
may itself also be a list. For example, the list [ this, is, a, list
] could also be written [ this | [ is, a, list ]] or
[ this, is | [ a, list ] ] or [ this, is, a | [ list
]] or [ this, is, a, list | [] ]. (In actual use,
the first or second part of the list, or both, will generally be a variable,
as in the earlier sorting example.)
Structures are used in several different ways in Prolog, with the meaning being determined by the context.
beagle(snoopy) might be used as a predication meaning
"snoopy is a beagle." (This use corresponds to the predicate calculus
notion of a predicate).
student(anthony, aardvark,
cs, 4.0) might be used to represent a student whose name is
Anthony Aardvark, whose major is cs, and whose gpa is 4.0.
+(1, 2) might be used as a function meaning "apply the
arithmetic addition operation to the arguments 1 and 2", and
sin(0.5) might be used as a function meaning "apply the
trignometric sine operation to 0.5". A set of
arithmetic functions is built into each
Prolog implementation, and cannot usually be extended by the user.
(This use is similar to the predicate calculus notion of a function,
except that it is restricted to arithmetic functions operating on
numbers, and the builtin functions have arity of 2 or less.)
Any sequence of alphanumeric characters (including the underscore) which
begins with an uppercase letter or the underscore is recognized as a variable -
e.g.
A
This_Is_A_2nd_Variable
However, variable names that consist of an underscore followed by a number
(e.g. _0 or _123) are generated internally by the
implementation, and should not be used in programs.
When the same variable name occurs more than once in a construct, it is the
expectation that will refer to the same object each time it occurs. There is
one exception to this - an underscore all by itself (_) is called
the anonymous variable, and is regarded as a different variable (and hence can
refer to different objects) each time it occurs in a given construct. For
example, in the construct dog(X) :- beagle(X) (meaning "something
is a dog if it is a beagle"), the variable X must refer to the
same object in both uses; but if it were written as
dog(_) :- beagle(_), the two uses of the anonymous variable would
not need to refer to the same object - so the meaning would boil down to
"anything is a dog as long as there is some object that is a beagle."
At any given time, a Prolog variable is in one of two states: uninstantiated, or instantiated. An uninstantiated variable has no value; an instantiated variable has as its value a constant or a structure, and means exactly the same thing as its instantiation. (In fact, in documentation it is common to find a phrase like "thus and such is an atom", which means that "thus and such is an atom, or a variable that has been instantiated to an atom".) During computation, an uninstantiated variable may become instantiated; howver, once a variable has been instantiated it cannot be instantiated to anything different while computation proceeds forward. It is also possible for two instantiated variables to share with one another - which simply means that if one becomes instantiated, then the other immediately becomes instantiated to the same thing.
As noted above, whenever a variable appears in a predication, it is to be understood in one of two senses
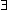 ), meaning that there exists some value for which
the predication is true.
), meaning that there exists some value for which
the predication is true.
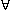 ), meaning the predication is true for all values
the variable may assume.
), meaning the predication is true for all values
the variable may assume.
At any given time, the Prolog system has a database which consists of a collection of clauses that are either rules or facts.
Rules correspond to what are called Horn clauses in predicate logic (though the
correspondence is not immediately apparent, and it is possible to formulate a
rule that does not correspond to a Horn clause). In Prolog, rules have the form
Head :- Body, where Head is either a structure or
(more rarely) an atom, and the rule means "The head is true if the body is
true." For example, we have already noted that the rule "something is a dog if
it is a beagle" can be represented by the Prolog rule dog(X) :-
beagle(X). Often, though, the body of a rule consists of several
predications joined by , (as in the earlier sorting example),
which in this context means logical conjunction (and) - e.g. a rule of the
form chases(D, C) :- dog(D), cat(C) says that "something chases
something else if the first something is a dog and the second is a cat."
Facts are simple predications - for example, the fact that snoopy is a beagle
might be represented in Prolog by beagle(snoopy). Though
infrequent, it is also possible for an atom to be recorded in the database as a
fact - e.g. some program might record the fact input_done in the
database to indicate that it has finished reading input.
Actually, facts are stored in the database as rules whose body is
the atom true - a predication which is, of course, always true.
Thus beagle(snoopy) is equivalent to - and would be stored as -
beagle(snoopy) :- true, which says in effect that "snoopy is a
beagle if true is true".
Variables which appear in rules are understood to be universal variables.
Thus, in the rule dog(X) :- beagle(X), the variable X
is understood as meaning "for all X" - but since the same variable appears in
both the head and the body, its universality is constrained by the fact that
the body predication must be true for any chosen value. (For this reason, it
is rare to find a variable in a fact.) Moreover, the variables that appear in
any given rule are strictly local to that rule; if another rule uses a variable
with the same name, they are not the same variable.
Two terms are said to unify if they are the same, or can be made to be the same by some instantiation of uninstantiated variables in either or both terms. The instantiation(s) that make the terms unify is called a unifying substitution or a unifier. If there is more than one possible substitution, Prolog uses the most general unifier - the one that is least constraining on the variables.
a(b, c) and a(b, c) unify because they
are, in fact, the same.
a(b, X) and a(Y, c) unify with
unifier X instantiated to c and Y
instantiated to b.
a(b, X) and a(X, c) don't unify
because there is no way of instantiating X to a single value
that makes both terms the same.
The Prolog system performs unification automatically as part of the process
of proving a goal, as discussed below. It is also possible to explicitly
request unification by the use of the unification operator =.
For example, a(b, X) = a(Y, c) succeeds by instantiating
code>X to c and Y to b. Note
well that unification is not at all the same as assignment or
comparison even though it uses a symbol (=) that often
has that meaning in other programming languages, and sometimes has an effect
that is similar to either assignment or comparison. For example, the following
two lines of Prolog code are absolutely identical in meaning, and (viewed as
comparisons) are both true, provided X was uninstantiated prior
to executing the statement.
X = ameans exactly the same thing as
a = X
Prolog also provides a "not unifiable" operator (\=) which
succeeds just when two terms cannot be unified.
Prolog computation involves proving a goal (a structure or an atom) using the clauses in the database. Variables appearing in the goal are taken as existential variables, and the proof typically finds instantiations for them which make the goal true. The proof process makes use of a stack of goals. The following is the core of the process:
As an illustration, suppose the database contains the following clauses:
beagle(snoopy). cat(garfield). cat(sylvester). dog(X) :- beagle(X). dog(butch). fierce(butch). chases(D, C) :- dog(D), cat(C).We can formulate the question "Who chases whom?" as the goal
chases(Chaser, Chasee). Starting this with the initial goal, we
find that it unifies with the head of the final rule. Now our goal stack
contains two goals: dog(Chaser) and cat(Chasee). The
first goal unifies with the head of the "dog if beagle" rule. Now our goal
stack still contains two goals, though the top goal is now different:
beagle(Chaser) and cat(Chasee). The first goal
unifies with the first fact with substitution snoopy for
Chaser. The second goal unifies with the second fact with
substitution garfield for Chasee. Since the goal
stack is now empty, we announce success with the answer "snoopy chases
garfield". (No one said that the Prolog database has to conform to reality :-))
Sometimes, there is more than one way to accomplish the step "Find a fact or a
rule whose head will unify with the goal." In this case, the Prolog proof
engine chooses the first possible clause. Sometimes, such a choice
leads to failure of the proof, though the proof would have succeeded if a
different choice had been made. For example, suppose our "chases" rule were
chases(D, C) :- dog(D), fierce(D), cat(C). In this case, after
discovering that snoopy is a dog, our goal stack would contain
fierce(snoopy) and cat(Chasee). Of course, there is
no clause that allows the first of these to be satisfied.
To deal with situations like this, the Prolog proof engine keeps track of
choicepoints - places where there were two or more clauses that could have been
chosen. If there are any outstanding choicepoints, then upon the failure of
the top goal on the stack, the proof engine backtracks to the most recent
choicepoint still having alternatives, tries another alternative instead, and
proceeds as if it had been chosen in the first place. (Alternatives are
considered in the order in which the clauses occur in the database.) In the
example, once fierce(snoopy) fails, the proof engine backtracks to
the place where it chose dog(X) :- beagle(X) to satisfy
dog(Chaser) and instead chooses dog(butch) for this
purpose. Since fierce(butch) corresponds to a fact in the
database, the proof proceeds with answer "butch chases garfield."
When backtracking takes place, any instantiations done by the choice that is
being redone, or since that choice was made, are undone - i.e. the variables
involved become uninstantiated again. In the example above, the instantiation
of Chaser to snoopy is undone so that it can be
instantiated instead to butch.
There is a second situation under which backtracking occurs. After the proof
engine has announced success, the user has the option to either accept the
answer given or to request the proof engine to try to find more solutions.
(This choice is made by entering ; - the Prolog symbol for "or" -
before pressing return when success is announced). The proof engine then
backtracks to the last open choicepoint, and proceeds to try to find a
different solution. For example, in this case the proof engine would backtrack
to the point where it found cat(garfield) as a fact that unified
with the goal cat(Chasee), and would instead choose the fact
cat(sylvester) leading to the new solution "butch chases
sylvester". (If the user requested another solution at this point, the proof
would fail since all possibilities have been exhausted.)
Though Prolog is based on formal logic in the form of the predicate calculus, the language includes various facilities that are needed to allow it to be a practical programming language. These are provided by various builtin predicates. Step two of the proof procedure outlined above contains an additional test:
A builtin predicate may succeed or fail; if it fails, backtracking is initiated
just as it is by the failure to find a clause that matches a goal. Moreover,
some builtin predicates themselves create choicepoints if there is more than
one way to satisfy the builtin - for example, the builtin predicate
retract/1 removes the first clause that unifies with its argument
from the database, and can be redone as many times as there are candidate
clauses.
not and the ISO dialect calls
it \+.) (Click here
for a discussion of the builtin predicates that are part of the PrologJ
implementation, which includes both the Edinburgh and ISO dialects plus several
more.)
The discussion below includes many but by no means all the builtin predicates that might be found in a Prolog implementation.
The set of Prolog builtin predicates includes facilities for modifying and
inspecting the database. ISO Prolog requires that any predicate that is to
be modified must be explicitly declared dynamic before any
clauses for it appear; and any predicate that is to be inspected by
clause/2 must be declared public unless it has
been declared dynamic. (Edinburgh Prolog does not have the
concept of dynamic or public predicates, and therefore does not have these
requirements - all user-defined predicates can be modified or accessed as
described here.)
asserta/1 - Add a new fact or rule to the database,
before any other clauses with the same functor and arity.
assertz/1 - Add a new fact or rule to the database,
after any other clauses with the same functor and arity.
clause/2 - Access the first rule whose head and body unify
with the two arguments of the predicate. (Recall that a fact
is equivalent to a rule whose body is true.) This
predicate establishes a choicepoint that allows accessing subsequent
rules during backtracking.
deny/1 - Delete from the database all facts or rules
for a specified functor and arity.
retract/1 - Delete from the database the first fact
or rule that unifies with the argument. If the argument of
retract/1 is of the form :-/2, then a rule
is sought whose head unifies with the first subargument and whose body
unifies with the second; otherwise a rule whose body is
true (a fact) is sought. This predicate establishes
a choicepoint that allows retracting subsequent rules during
backtracking.
retractall/1 - Delete from the database all
facts or rules that unify with the argument. The argument is
interpreted the same way as it is for retract/1; but of
course no choicepoint needs to be established because all matching
entries in the database are deleted.
Each of these takes a single argument, and succeeds if the argument is of the
specified type and fails otherwise. Although it is legal to apply one of these
predicates to a constant or structure, its argument is usually a variable and
the predicate tests the type of its instantiation or (except for
nonvar/1) fails if the argument is uninstantiated.
atom/1 - succeeds if the argument is an atom.atomic/1 - succeeds if the argument is an atom or number.compound/1 - succeeds if the argument is a structure.float/1 - succeeds if the argument is a real number.integer/1 - succeeds if the argument is an integer.nonvar/1 - succeeds if the argument is an instantiated
variable, or anything other than a variablenumber/1 - succeeds if the argument is a float or an integer.
var/1 - succeeds if its argument is an uninstantiated variable.
(This is the only metalogical predicate that succeeds
for an uninstantiated variable; it fails for anything
else.)These allow accessing the parts of a structure, or constructing a structure, in various ways
arg(N, Term, Arg) - unifies Arg with the
nth argument of Term. Argument number is 1-origin.
functor(Term, Functor, Arity) - unifies Functor
with the functor of Term and Arity with its
arity. (This builtin may be used with an atomic term, in which case
the term is considered its own functor, and the arity is
0.) If Term is uninstantiated but the other
two arguments are instantiated, this builtin constructs a term having
the specified functor with the specified number of fresh variables as
arguments, or a constant if the arity specified is 0.
=.. (pronounced "univ") converts between a structure
and a list whose first element is the functor of the structure, and
whose remaining elements are its arguments. The process is
bidirectional; =.. can be used to convert a structure to
a list or a list to a structure. It can also be used with an atomic
term, which is converted to/from a 1-element list. For example,
dog(snoopy) =.. L instantiates L to the
list [ dog, snoopy ] and S =.. [ dog, snoopy ]
instantiates S to dog(snoopy).
We have already noted that Prolog defines a large number of arithmetic functions, including the familiar arithmetic operations +, -, *, /. An expression composed of these functions is evaluated in one of two ways:
is/2 - in which case it is
evaluated and the first argument is unified with the result - e.g.
X is 1 + 2 unifies X with 3.
=:=, =\=, <,
=<, >, >=). Each
of the arguments of one of these comparisons is evaluated, and then
the results are compared - e.g. 2 + 2 =:= 1 + 3 succeeds.
Note the peculiar way =< is written!
These predicates allow the comparison of any two terms. The relational comparisons are based on an ordering relationship known as term-preceeds, which yields a total ordering of terms. In the case to two numbers of the same type (integer or float) this ordering is the same as normal arithmetic ordering; but a float always tests "less than" an integer.
== - two terms identical. This is not at all the same as
unification (=), rather it tests to see whether two terms
are already the same, without performing any unifications. (Of course,
in the case of two terms that contain no uninstantiated variables,
both = and == mean exactly the same thing.)
\== - two terms not identical. This is true just when
== is false and vice versa. This is not at all the same as
not unifiable (\=), rather it tests to see whether two
terms are not currently the same, regardless of whether they could be
made the same by unification. (Of course, in the case of two terms that
contain no uninstantiated variables, both \= and
\== mean exactly the same thing.)
@< - the first term precedes the second in the term
precedes relationship.
@=< - the first term precedes or is identical to the
second in the term precedes relationship. Note the way this is written!
@> - the first term follows the second in the term
precedes relationship.
@>=; - the first term follows or is identical to the
second in the term precedes relationship.
Prolog includes a large number of predicates for doing input/output. Most input predicates read either a single character or a term and unify the result with an argument. Most output predicates always succeed, but have the side effect of writing either a single character or a term. ISO Prolog provides two versions of most IO predicates; one reads or writes to the current input or output stream, and the other takes a "stream term" as an additional first argument. Some are specific to one or the other of the two dialects; others are common to both.
In a list of Prolog predicates, Most IO predicates can be recognized by having
names that begin with get (single character or byte read),
peek (single character or byte lookahead without reading),
read (full term read), put (single character or
byte write), or write (full term write.) (However, there are other
IO predicates as well.)
We have already noted that the body of a Prolog rule often consists of a
series of predications joined by commas. In this context, , is
an atom, not a punctuation mark, and ,/2 is regarded as a
predication corresponding to logical conjunction (and) - i.e. ,/2
is true just when both of its arguments are true. [Arguably, it is a bit
confusing to find the same character used both as a punctuation mark and as
an atom in different contexts!] Prolog provides a number of other logical
operators as well, plus control structures that move beyond pure logic.
GoalA, GoalB - logical conjunction (and). True when both
GoalA and GoalB are true. On backtracking,
alternatives for GoalB are explored, and if no available
alternative succeeds then an alternative for GoalA is
sought; if one is found then GoalB is tried again.
GoalA ; GoalB - logical disjunction (or). True when
either GoalA or GoalB is true, with
GoalA being tried first and GoalB
being tried only if it fails. On backtracking, alternatives for
whichever subgoal succeeded are explored; if this was GoalA
and no available alternative succeeds then GoalB is tried.
not Goal (Edinburgh) or \+ Goal (ISO) -
logical negation (not). Goal is tried and if it succeeds
the "not" goal fails; if Goal fails then the "not" goal
succeeds.
Condition -> Then - logical if-then. Condition
is tried and if it succeeds then Then is tried and if
it succeeds too, the "if-then" goal succeeds. However, if
Condition fails, then Then is not tried, and
the "if-then" goal fails. On backtracking, Then can be
redone, but not Condition. Note that this looks
like logical implication (also denoted ->), but it is
not; a logical implication of the form A -> B succeeds
if A fails, but a Prolog "if-then" fails if the condition fails.
Condition -> Then ; Else - logical if-then-else.
Condition is tried and if it succeeds then
Then is tried, but if it fails Else is
tried instead. If whichever of the two possibilities that is tried
succeeds too, the "if-then-else" goal succeeds. On backtracking,
whichever of Then or Else that was tried can
be redone, but not Condition or the decision as to
which alternative to try. Note that logical implication (also
denoted ->) is equivalent to Prolog A -> B ; true.
repeat - a primitive looping construct. When initially
called, repeat succeeds; and on backtracking, it
succeeds again (unless cut as discussed below). This can be used
with a series of goals and an end test to form a "repeat-until" sort
of loop - e.g. the following would read individual characters and
print their ASCII codes until '.' is processed:
repeat, get(C), % Reads a character and unifies C with its ASCII code write(C), nl, C = 46. % 46 is the ASCII code for '.'
ISO Prolog defines a facility that can be used for handling errors. It
uses two builtin-predicates: throw/1 and catch/3.
An error is signalled by throwing a "ball" - a term which is descriptive of
the error. The Prolog implementation does this automatically for various
error conditions, but the user can also do so by using throw/1.
When a ball is thrown, the system searches for the nearest ancestor
catch/3 goal that can catch it; if there is no such ancestor then
the Prolog system itself reports the error (in much the way that an uncaught
exception is handled in a language such as Java.) This is perhaps best
illustrated by an example - a program that classifies individual letters as
either a vowel or a consonant. (Actually, the approach here is a bit
non-elegant, but this is meant to illustrate a the concept being discussed here
and the cut to be discussed next.)
classify :-
repeat,
write('Please enter a letter to classify: '),
get_char(L), skipln,
catch(classify(L, C), not_letter, C = 'Not a letter'),
write(C), nl,
L = z.
classify(L, 'Vowel') :-
member(L, [ a, e, i, o, u ]),
!.
classify(L, 'Consonant') :-
member(L, [ b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, z ]),
!.
classify(y, 'Either a vowel or a consonant') :-
!.
classify(_, _) :-
throw(not_letter).
member(H, [ H | _ ]) :- !.
member(E, [ _ | T ]) :- member(E, T).
The arguments of catch/3 are a goal to be called initially, a term
to be unified with a ball that might be thrown while executing this goal, and a
goal to be called if a ball was caught.
!)Sometimes, it is desirable to preclude backtracking that might otherwise occur. This is illustrated by the above example.
classify/0, a series of steps are performed repeatedly
until the program is asked to classify the letter z.
L = z, which fails unless the user entered z.
L = z fails, we want to go back to the
repeat and start the whole process over.
classify/2 does create a choicepoint. In
particular, the final rule relies on the fact that rules are tried
in the order in which they appear in the database, so that an error
is reported only if the character the user entered failed the Vowel,
Consonant, and "y" tests. However, during backtracking we
would ordinarily end up trying this rule regardless of the character
entered, resulting in falsely declaring every letter
(except the terminator, z) to be 'Not a letter' before asking the
user to enter another one.
This problem could be prevented by adding explicit tests to the final rule to rule out the possibility that the character the user entered is really good - i.e. it could read something like:
classify(L, _) :-
not member(L, [ a, e, i, o, u ]),
not member(L, [ b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, z ]),
L \= y,
throw(not_letter).
However, this solution is ugly and inconvenient, to say the least! Instead,
each of the preceeding rules makes use of the builtin predicate cut
(!/0), which is defined as follows:
!/0 simply succeeds.!/0 cuts off choicepoints all the
way back to the time the clause of which it is a part was chosen.
Thus, when the conditions for any of the first three classify/2
rules is satisfied, the !/0 contained in the rule ensures that no
alternative for classify/2 will be considered during backtracking.
To see the difference this makes, consider what happens if we try a version of
the program that does not contain cuts - i.e. if the classify/2
rules were as follows:
classify(L, 'Vowel') :-
member(L, [ a, e, i, o, u ]).
classify(L, 'Consonant') :-
member(L, [ b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, z ]).
classify(y, 'Either a vowel or a consonant').
classify(_, _) :-
throw(not_letter).
If the program include this version of the classify/2 rules
instead, it would print the correct classification for a letter, and then - on
the next line - would print 'Not a letter' for any letter except z.
It is important to bear in mind that ! cuts off every
choicepoint established since the choice of the clause in which it occurs, as
well as the clause choice itself. Suppose we used the "cut-less" version of
the classify/2 rules as above, but instead tried to put the cut
in the main rule, like this:
classify :-
repeat,
write('Please enter a letter to classify: '),
get_char(L), skipln,
catch(classify(L, C), not_letter, C = 'Not a letter'),
write(C), nl,
!,
L = z.
This program would not erroneously report that a letter is 'Not a letter',
because the ! would cut off the choice made for the
classify/2 rule, just like embedding it in the rules would.
However, it would also cut off the choicepoint for repeat/0,
with the consequence that the program would now always terminate after the user
entered just one character!
The builtin predicate cut is, at the same time, a powerful tool for preventing unwanted results during backtracking and a dangerous tool that, if misused, can prevent correct results from being found by precluding the exploration of alternatives that should be considered. (Cut is the Prolog equivalent of a chain saw!) The place where cut is most useful is when a predicate is defined by a series of rules, of which only one should apply to a given case. In such a case, cut is often inserted immediately after the tests that determine the case, to prevent exploration of subsequent, unnecessary (and possibly erroneous) cases, as in the example just considered.
One other issue with regard to cut is the notion of "transparent to cut" versus
"opaque to cut". Some of the control structure predicates are opaque to cut -
meaning that if a cut occurs in a subgoal, it has no effect on any ancestor of
the opaque goal. However, ,/2 and ;/2 are both
transparent to cut - if they weren't the above example would not have worked,
because the cut in the various classify/2 rules would have been
blocked. Of the control structures we have considered:
,/2 is transparent to cut;/2 is transparent to cutnot/1 or \+/1 is opaque to cut->/2 and -> ; / 3 are transparent to cut
in their "then" and "else" parts, but opaque to cut in their
"condition" part.
repeat/0 is irrelevant, since it doesn't actually have
subgoals in the way these other predicates do.)
catch/3 is opaque to cut
One other control structure predicate that is used precisely because it is
opaque to cut is call/1, which simply calls a goal and succeeds
just when the goal succeeds. Indeed, were it not for the fact that it is
opaque to cut, this builtin would serve no good purpose, since its behavior
is otherwise equivalent to simply calling the subgoal!